07/20/2020 Algorithms
重新思考二分法/二分插入排序
起因是leetcode315. 计算右侧小于当前元素的个数
给定一个整数数组nums,按要求返回一个新数组counts
数组counts有该性质:counts[i]的值是nums[i]右侧小于nums[i]的元素的数量
示例:
输入:[5,2,6,1]
输出:[2,1,1,0]
解释:
5 的右侧有 2 个更小的元素 (2 和 1)
2 的右侧仅有 1 个更小的元素 (1)
6 的右侧有 1 个更小的元素 (1)
1 的右侧有 0 个更小的元素
该题最简单的解法是Brute force,两层循环判断第二层循环的元素是否小于第一层循环的元素,简单明了,但作为一道Hard题目,显然这种方法会超时
一般解法中,有从后往前使用插入排序的,也就是说,假定后半部为有序,从倒数第二位起,将元素在有序子集中找到合适的位置进行插入,并记录移动了多少位,得出结果数组
插入排序时间复杂度也是$O(n^2)$,同样会超时,需要进行优化,而直接插入排序的一般优化方法就是使用二分法来找到合适的插入位置,可以将查找的时间复杂度降为$O(log_{2}n)$
然而在写二分插入排序的过程中,对上下边界处理屡屡出错,不得正解,于是重新实验,归纳总结,形成模板,死记硬背
查找
对于一个从小到大的有序数组nums,比较目标值target和集合中间元素nums[mid]的大小
- 如果
nums[mid] < target,说明target应该在后半部分 - 否则说明
target应该在前半部分
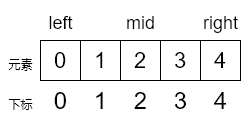
对于数组或其前半/后半子集的起点和终点,假设用left和right表示,初始则有
int left = 0;
int right = nums.length - 1;数组下标范围是[0, nums.length - 1]闭区间
但也可以使用[0, nums.length)左闭右开区间
int left = 0;
int right = nums.length;使用不同的区间,后续流程的写法也不同
- 循环终止条件
随着子集划分越来越小,left和right也在不断靠近,直到重合,循环的条件应该写成while(left < right)还是while(left <= right)? - 子集的取值范围
缩小查找范围后,去左边区间时,left不变,right = mid - 1还是right = mid?
去右边区间时,right不变,left = mid + 1还是right = mid?
先从取值范围来看,如果一开始的取值使用了闭区间,子集的取值也应该是闭区间
if(nums[mid] < target) {
left = mid + 1;
} else {
right = mid - 1;
}如果一开始使用了左闭右开区间,子集的取值也应该是左闭右开区间
if(nums[mid] < target) {
left = mid + 1;
} else {
right = mid;
}target应该存在于[left, right)区间中,设target为集合的最后一个元素,区间即为[nums.length - 1, nums.length),left再增加会越界,循环应写成while(left < right)
同理在闭区间中,[nums.length - 1, nums.length - 1]是可以存在的,循环应写成while(left <= right)
交换
对于排序来说,找到合适的位置后,就要将元素插入到该位置上,而合适的位置是查找阶段得出的left或right,它们是相等的,可以随便使用一个
通常对于一个集合插入排序来说,假定前半部分是有序的,即假设第一位是有序的,从第二位开始逐渐扩大有序集合,将当前元素与前面的元素做交换,直到插入到有序的前半部分中合适的位置
那么就是从当前位置到left,从后往前做交换了
int x = nums[i];
//查找部分省略
//交换
for(int j = i; j > left; j--) {
nums[j] = nums[j - 1]; //从后往前每个元素往后移动一位
}
nums[left] = x;使用golang将正序、逆序、从后往前、从前往后、假定前部有序、假定后部有序的的二分插入排序都实现了一遍,都使用了闭区间
package algo
//BinaryInsertionSort 插入排序时使用二分法搜索插入位置
//二分搜索的基本条件是确保集合有序
//那么首先就要假定数组的一部分是有序的
//假定当前下标之前有序
func BinaryInsertionSort(arr []int) {
len := len(arr)
for i := 1; i < len; i++ {
x := arr[i]
left := 0
right := i - 1
for left <= right {
mid := left + (right-left)/2
//x位置在mid右边
//x < arr[mid],希望正序排列,所以要去左边的区间找x的位置
if x < arr[mid] {
right = mid - 1
} else {
left = mid + 1
}
}
//j一定大于left
//正序排列,前部为假定的有序区间
//候选的位置是left
//那么left和它之前的元素全部向前移动一位
for j := i; j > left; j-- {
arr[j] = arr[j-1]
}
arr[left] = x
}
}
//BinaryInsertionSort1 倒序实现
func BinaryInsertionSort1(arr []int) {
len := len(arr)
for i := 1; i < len; i++ {
x := arr[i]
left := 0
right := i - 1
for left <= right {
mid := left + (right-left)/2
//x位置在mid右边
//x > arr[mid],希望倒序排列,所以要去左边的区间找x的位置
if x > arr[mid] {
right = mid - 1
} else {
left = mid + 1
}
}
for j := i; j > left; j-- {
arr[j] = arr[j-1]
}
arr[left] = x
}
}
//BinaryInsertionSort2 反向遍历实现
func BinaryInsertionSort2(arr []int) {
len := len(arr)
//假定后面的是有序的,且正序排列
for i := len - 2; i >= 0; i-- {
x := arr[i]
left := i + 1
right := len - 1
for left <= right {
mid := left + (right-left)/2
if x > arr[mid] {
//x应该去mid右边找位置
left = mid + 1
} else {
right = mid - 1
}
}
//j小于left
for j := i; j < left-1; j++ {
//[i, left]都要往前移一位
arr[j] = arr[j+1]
}
arr[left-1] = x
}
}
//BinaryInsertionSort3 reverse order, loop from end to start
func BinaryInsertionSort3(arr []int) {
len := len(arr)
for i := len - 2; i >= 0; i-- {
x := arr[i]
left := i + 1
right := len - 1
for left <= right {
mid := left + (right-left)/2
if arr[mid] > x {
left = mid + 1
} else {
right = mid - 1
}
}
for j := i; j < left-1; j++ {
arr[j] = arr[j+1]
}
arr[left-1] = x
}
}需要注意的是,反向遍历得出的位置left,使用的时候需要减一