数据结构查找和排序复习

06/17/2020 Datastruct

查找

顺序查找

没什么说的，从头往后挨个儿匹配

时间复杂度$O(n)$
查找成功时概率为$1 \over n$平均查找长度为$(n + 1) \over 2$
查找不成功时平均查找长度为$n + 1$
成功和不成功概率为$1 \over 2$

int search(int[] array, int target) {
    for(int i = 0; i < array.length; i++) {
        if (array[i] == target) {
            return i;
        }
    }
    return -1;
}

有序表的查找Binary Search

数据自带顺序，可以使用二分查找

时间复杂度$O(log_{2}n)$
平均查找长度$log_{2}n + 1$

int binSearch(int[] array, int target) {
    int low = 0;
    int high = array.length - 1;
    while(low <= high) {
        int mid = (low + high) / 2;
        if(target == array[mid]) {
            return mid;
        }
        if(target > array[mid]) {
            low = mid + 1;
        }else{
            high = mid - 1;
        }
    }
    return -1;
}

二叉查找树BST

对于二叉查找树，左子节点的值小于根节点，右子结点的值大于根节点
需要先构建树 [5, 8, 4, 6, 1, 3, 2, 7]

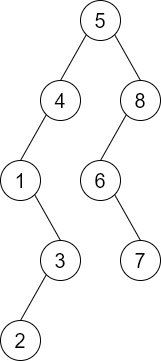
查找成功时的平均查找长度：$$(1 \times 1+ 2\times 2+3\times 2+4 \times 2+5 \times 1) \over 8$$

对于有序数据，可以直接从中间开始构建二叉查找树

class Node {
    Integer data;
    Node left;
    Node right; 
}

//构造
Node BST(int[] array) {
    Node root = new Node();
    for(int i = 0; i < array.length - 1; i++) {
        put(node, array[i]);
    }
    return root;
}

//递归实现
void put(Node node, Integer data) {
    if(node.data == null) {
        node.data = data;
    } else {
        if(data < node.data) {
            if(node.left == null) {
                node.left = new Node();
                node.left.data = data;
            }else{
                put(node.left, data);
            }
        }else{
            if(node.right == null) {
                node.right = new Node();
                node.right.data = data;
            }else{
                put(node.right, data);
            }
        }
    }
}

//查找递归实现
boolean search(Node node, int target) {
    if(node == null) {
        return false;
    }
    if(target == node.data) {
        return true;
    }
    if(target < node.data) {
        return search(node.left, target);
    }else{
        return search(node.right, target);
    }
    
}

hash查找

建立key与数据的映射关系，将key经过hash后存储

一些hash方法

直接定址法：直接取key或key的线性函数
数字分析法：分析key，取若干位组成hash值
平方取中法：key平方后取中间几位
折叠法：分割key并叠加
除留余数法：k mod size(hashmap)

解决hash冲突

hash冲突：当$key_1 \neq key_2$时$hash(key_1) = hash(key_2)$

开放定址法$hash = hash(key + d_i) mod size(hashmap)$
1. 线性探测再散列：$d_i$为线性值$d_i = 1, 2, 3….$
2. 二次探测再散列：$d_i = \pm k^2$
3. 伪随机探测再散列：$d_i = random$
再hash：hash(hash(key))
链地址法：发生冲突时将相关的key组成链表
公共溢出区：发生冲突时插入溢出表

Java的HashMap使用了链地址法，在Java8前使用普通的链表，Java8之后，默认如果链表的长度超过8，则转为红黑树，将时间复杂度从$O(n)$变为$O(log n)$

排序

评估标准：时间效率、空间效率、是否稳定

时间效率：循环的次数
空间效率：局部变量大小
稳定：相同的元素不会改变位置

直接插入排序Straight Insertion Sort

稳定
最坏性能：$O(n^2)$次比较和交换
最好性能：数据基本有序$O(n)$次比较，$O(1)$次交换
平均性能：$O(n^2)$次比较和交换
辅助空间：$O(1)$

void insertionSort(int[] array) {
    for (int i = 1; i < array.length; i++) {
        int x = array[i];
        int j = i - 1;
        // 如果前面的数比后面的数字大，前面的数往后移一位
        while(j >= 0 && array[j] > x) {
            array[j + 1] = array[j];
            j = j - 1;
        }
        // 将当前值插入合适的位置
        array[j + 1] = x;
    }
}

折半插入排序Binary Insertion Sort

直接插入排序从后往前找插入位置，而折半插入排序在已排好序的数据中进行折半查找确定插入位置

最坏性能：$O(n^2)$次比较和交换
最好性能：$O(nlogn)$次比较，$O(1)$次交换
平均性能：$O(n^2)$次比较和交换
辅助空间：$O(1)$

void binInsertionSort(int[] array) {
    for (int i = 1; i < array.length; i++) {
        int x = array[i];
        // 使用二分查找
        int low = 0;
        int high = i;
        while (low < high) {
            int mid = (low + high) / 2;
            if (x >= array[mid]) {
                low = mid + 1;
            } else {
                high = mid;
            }
        }
        // 将当前值插入合适的位置
        // 将该位置后开始到i的数据全部往后移一位再将x插入该位置
        //for (int j = i - 1; j > low - 1; j--) {
        //    array[j + 1] = array[j];
        //}
        //array[low] = x;
        // 或者从后往前，把x一个一个的交换到指定位置
        for (int j = i; j > low; j--) {
            int tmp = array[j - 1];
            array[j - 1] = array[j];
            array[j] = tmp;
        }
    }
}

希尔排序Shell Sort

将待排序列按一定步长分为若干子序列分别进行直接插入排序，再进行全部数据的插入排序

不稳定
最坏性能：按步长不同性能不同，最常见的为$O(n{log^2}n)$
最好性能：$O(nlogn)$
平均性能：按步长不同性能不同
辅助空间：$O(1)$

void shellSort(int[] array) {
    // gap为array.length / 2，array.length / 4 ...逐渐缩小
    for(int gap = array.length / 2; gap > 0; gap /= 2) {
        for (int i = gap; i < array.length; i++) {
            int x = array[i];
            int j = i;
            //从后往前每隔gap取一个数据进行插入排序
            while(j >= gap && array[j - gap] > x) {
                array[j] = array[j - gap];
                j = j - gap;
            }
            array[j] = x;
        }
    }
}

冒泡排序Bubble Sort

一次遍历把一个最值放在一端，性能很差，只做学习用

稳定
最坏性能：$O(n^2)$次比较和交换
最好性能：$O(n)$次比较$O(1)$次交换
平均性能：$O(n^2)$次比较和交换
辅助空间：$O(1)$

void bubbleSort(int[] array) {
    for (int i = 0; i < array.length - 1; i++) {
        for (int j = 0; j < array.length - 1 - i; j++) {
            if(array[j] > array[j + 1]) {
                int tmp = array[j + 1];
                array[j + 1] = array[j];
                array[j] = tmp;
            }
        }
    }
}

快速排序Quick Sort

快速排序是分治算法（divide and conquer），每次循环选定一个数据作为轴pivot，该轴在本次循环内不变，比轴小的数据和轴交换位置，一次循环可以使比轴大的数据都集中到一侧，小的集中到另一侧，再对每侧子集进行快速排序，这样子集有序时，整个数据集就有序了。

轴的选择影响算法效率，如果实现的恰当，可以比归并排序和堆排序快两到三倍
是一些编程语言的默认排序实现

高效实现是不稳定的
最坏性能：$O(n^2)$很少见
最好性能：$O(nlogn)$
平均性能：$O(nlogn)$
辅助空间：与实现有关

// 递归模板
void quickSort(int[] array, int low, int high) {
    if (low < high) {
        int j = partition(array, low, high);
        quickSort(array, low, j - 1);
        quickSort(array, j + 1, high);
    }
}

// 一个比较好理解的partition实现
// 用第一个元素做pivot
int partition(int[] array, int low, int high) {
    int pivot = array[low];
    int i = low;
    int j = high;
    while(i < j) {
        //从后往前找到一个小于pivot的
        while (i < j && array[j] > pivot) {
            j--; //跳过比pivot大的
        }
        if(i < j) {
            //交换
            array[i] = array[j]; //array[i]此时是pivot
            //其实这一步的正常做法是
            //int temp = array[i];
            //array[i] = array[j];
            //array[j] = temp;
            //但因为已经记录了pivot，所以省略了
            //此时可以将array[j]看作pivot
            //虽然它的值不是pivot
            i++; // 从下一位开始找比pivot大的
        }
        //从前往后找到一个大于pivot的
        while (i < j && array[i] < pivot) {
            i++; //跳过比pivot小的
        }
        if(i < j) {
            //交换
            array[j] = array[i];//这里把array[j]看作pivot
            //和上面相同，省略了显式的交换步骤
            //因为换来换去都是pivot
            j--;
        }
    }
    //i=j时跳出循环
    array[i] = pivot; //填上pivot
    return i;
}

选择排序Selection Sort

每次遍历选择出一个最值加入有序序列

是否稳定取决于实现
最坏性能：$O(n^2)$比较$O(n)$交换
最好性能：$O(n^2)$比较$O(n)$交换
平均性能：$O(n^2)$比较$O(n)$交换
辅助空间：$O(1)$

void selectionSort(int[] array) {
    for (int i = 0; i < array.length - 1; i++) {
        int index = i;
        for (int j = i + 1; j < array.length; j++) {
            if(array[j] < array[index]) {
                //选择小的
                index = j;
            }
        }
        if(index != i) {
            // 交换
            int temp = array[i];
            array[i] = array[index];
            array[index] = temp;
        }
    }
}

堆排序Heap Sort

简单的选择排序有重复比较的情况，堆排序对其进行改进

不稳定
最坏性能：$O(nlogn)$
最好性能：$O(nlogn)$或$O(n)$
平均性能：$O(nlogn)$
辅助空间：$O(1)$

先构建一棵完全二叉树，再进行调整，让任何非叶子结点的值都大于（或都小于）其左右子节点的值，堆顶一定是最值。

// 利用完全二叉树的性质
// 编号为i的结点，左孩子结点的编号为2i，右孩子结点的编号为2i+1 
// 为了不创建新结构，使用数组存储二叉树
void heapSort(int[] array) {
    // 因为完全二叉树编号为i的右子树结点为 2i+1
    // 所以 2i+1 <= array.length
    // 即 i <= array.length / 2 - 1
    int root = array.length / 2 - 1;
    int n = array.length - 1;
    for (int i = root; i >= 0; i--) {
        maxHeapify(array, i, n);
    }

    // 构建堆后，令数组有序
    // 每次移出根结点（与最后一个元素交换，再令堆的大小-1）
    for (int i = n; i > 0 ; i--) {
        int temp = array[0];
        array[0] =  array[i];
        array[i] = temp;
        maxHeapify(array, 0, i - 1);
    }
}

//小顶堆化
void maxHeapify(int[] array, int i, int n) {
    int li = i * 2 + 1; // 左子节点的下标
    if(li > n) {
        return; //没有子节点了
    }
    int ri = li + 1; // 右子节点的下标
    int j = li;
    //左右子节点谁小
    if(ri <= n && array[ri] > array[li]) {
        j = ri;
    }
    //子节点比父结点小就交换位置
    if(array[j] > array[i]) {
        int temp = array[i];
        array[i] = array[j];
        array[j] = temp;
        //交换了就要重新检查该数据与新的子节点之间的关系
        maxHeapify(array, j, n);
    }
}

归并排序Merge Sort

另一种分治算法，常用来和快速排序比较
将数据分成子集，对子集进行排序后，再归并成一个有序集合

稳定
最坏性能：$O(nlogn)$
最好性能：$O(nlogn)$变体可以达到$O(n)$
平均性能：$O(nlogn)$
辅助空间：$O(n)$用链表可以$O(1)$

有迭代法和递归法两种实现

迭代法（从下往上）：
1. 需要声明一个与原集合相同大小的辅助集合
2. 每相邻两个元素进行比较排序，形成$ceil(len/2)$个子集
3. 归并成每四个元素进行排序，形成$ceil(len/4)$个子集
4. 以此类推，直到排序完毕，集合数量为1

//迭代法实现
void mergeSort(int[] array, int[] reg) {
    int len = array.length;
    //令集合长度为2, 4, 8, 16...
    for (int width = 1; width < len; width *= 2) {
        //得到每个集合的起始下标
        for (int i = 0; i < len - 1; i += 2 * width) {
            int mid = i + width - 1;
            int high = i + 2 * width - 1;
            if(mid > len - 1) {
                mid = len - 1;
            }
            if(high > len - 1) {
                high = len - 1;
            }
            //合并array[i:i+width-1]和array[i+width:i+2*width-1]
            //当i + width > len - 1时，其实只剩array[i:len-1]了
            merge(array, reg, i, mid, high);
        }
    }
}

void merge(int[] array, int[] reg, int low, int mid, int high) {
    int i = low; //一个子集的起始下标
    int j = mid + 1; //另一个子集的起始下标
    int t = 0; //辅助集合下标
    while(i <= mid && j <= high) {
        if(array[i] <= array[j]) {
            //将小的元素插入辅助集合
            reg[t++] = array[i++]; //同时对应子集下标向后移一位
        }else{
            reg[t++] = array[j++];
        }
    }
    //如果子集还有剩下的元素，要放入reg中
    while (i <= mid) {
        reg[t++] = array[i++];
    }
    while (j <= high) {
        reg[t++] = array[j++];
    }
    //循环结束后，reg中就是基本有序且归并好的集合了
    t = 0;
    //把reg中的元素复制到源集合中，用有序的数据覆盖掉原来无序的相同数据
    while (low <= high) {
        array[low++] = reg[t++];
    }
}

递归法（从上往下）：
1. 需要声明一个与原集合相同大小的辅助集合
2. 归并前递归的将集合二分，归并中逐个下标的比较两个集合的数据并进行交换
3. 将两个集合归并，递归向上组成完整的有序集合

//递归模板
//和快速排序很像，不过快速排序先处理再递归，归并排序先递归再处理
void mergeSort(int[] array, int[] reg, int low, int high) {
    if(low < high) {
        int mid = low + (high - low) / 2;
        mergeSort(array, reg, low, mid);
        mergeSort(array, reg, mid + 1, high);
        merge(array, reg, low, mid, high);
    }
}

void merge(int[] array, int[] reg, int low, int mid, int high) {
    int i = low; //第一个子集的初始下标
    int j = mid + 1; //第二个子集的初始下标
    int t = 0; //辅助集合的下标
    while(i <= mid && j <= high) {
        if(array[i] <= array[j]) {
            //将小的元素插入辅助集合
            reg[t++] = array[i++]; //同时对应子集下标向后移一位
        }else{
            reg[t++] = array[j++];
        }
    }
    //如果子集还有剩下的元素，要放入reg中
    while (i <= mid) {
        reg[t++] = array[i++];
    }
    while (j <= high) {
        reg[t++] = array[j++];
    }
    //循环结束后，reg中就是基本有序且归并好的集合了
    t = 0;
    //把reg中的元素复制到源集合中，用有序的数据覆盖掉原来无序的相同数据
    while (low <= high) {
        array[low++] = reg[t++];
    }
}