一些概念

• 图：图结构中，任意两个结点之间的关系是任意的
• 顶点：图的数据
• 边：顶点之间的关系
• 弧：有方向的边
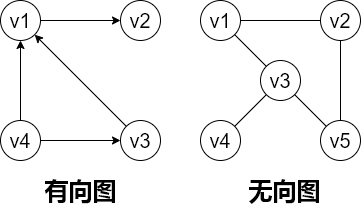
• 有向图（digraph）：有向图$G_1=(V_1,A_1)$，其中$V_1=\{v1,v2,v3,v4\}$，$A_1=\{<v1,v2>,<v1,v3>,<v3,v4>,<v4,v1>\}$
• 无向图（undigraph）：无向图$G_2=(V_2,E_2)$，其中$V_2=\{v1,v2,v3,v4,v5\}$, $E_2=\{(v1,v2),(v1,v3),(v2,v5),(v3,v5),(v3,v4)\}$

• 无向图顶点数$n$与边$e$的关系：
  $$0 \leq e \leq \frac{1}{2} n(n-1)$$
• 有向图顶点数$n$与弧$e$的关系：
  $$0 \leq e \leq n(n-1)$$
• 完全图：有$\frac{1}{2} n(n-1)$条边的无向图
• 有向完全图：有$n(n-1)$条弧的有向图
• 稀疏图：只有顶点的图
• 稠密图：边很多的图
• 子图：有一个图的顶点属于原图，边也属于原图
• 邻接点：无向图中，两个顶点右边，则互为邻接点
• 顶点的度：与该顶点相关联的边的条数
• 出度：有向图中，以该顶点为起点的弧的条数
• 入度：有向图中，以该顶点为重点的弧的条数
• 有向图顶点的度=该顶点的出度+入度
• 路径
• 简单路径：顶点序列中，顶点不重复的路径
• 回路：路径的起点和终点相同
• 连通图：无向图中，任何两个顶点之间都有路径
• 连通分量：非连通图中的一个部分
• 强连通图：有向图中，任何两个顶点之间来回都有路径
• 强连通分量：非强连通图中的一个部分
• 一个连通图的生成树：一个极小连通子图含有图的所有$n$个结点和$n-1$条边
• 一棵有个$n$个顶点的生成树有$n-1$条边，但有$n-1$条边的图不一定是生成树
• 有向图的生成树：一个顶点的入度为0，其余顶点的入度都为1

---

图的存储结构

任何数据结构都可以用顺序存储和链式存储

邻接矩阵

使用两个数组分别存放顶点信息和边（弧）信息

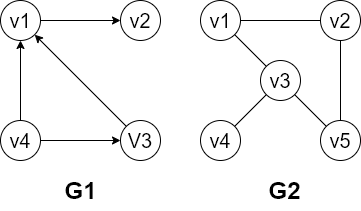
$$G1.vtxs=[v1, v2, v3, v4]$$ $$G1.arcs=\begin{bmatrix}0 & 1 & 1 & 0 \\ 0 & 0 & 0 & 0 \\0 & 0 & 0 & 1 \\1 & 0 & 0 & 0 \end{bmatrix}$$ $$G2.vtxs=[v1, v2, v3, v4, v5]$$ $$G2.arcs=\begin{bmatrix}0 & 1 & 1 & 0 & 0\\ 1 & 0 & 0 & 0 & 1\\1 & 0 & 0 & 1 & 1 \\0 & 0 & 1 & 0 & 0 \\0 & 1 & 1 & 0 & 0 \end{bmatrix}$$
可以发现都是以左上到右下的轴对称的矩阵

使用数组存储，浪费存储空间

邻接矩阵的性质

• 对于无向图来说行的和为该顶点的度
• 对有向图来说行的和为顶点的出度，列的和为顶点的入度

网

带权的邻接矩阵
权替代1 无限大替代0

邻接表

为图的每一个顶点创建一个单链表，链表中的结点为依附于顶点的边

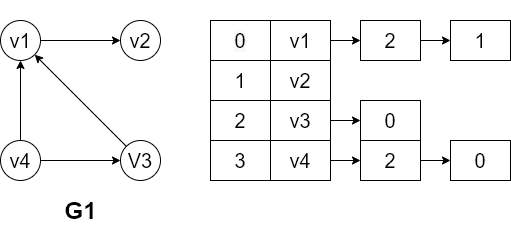
对于有向图来说，该邻接表为出边表，它的逆邻接表为入边表

邻接表的性质

• 无向图邻接表中，顶点的度为对应的单链表的节点总数
• 有向图邻接表中，顶点对应的链表的结点总数为该顶点的出度，入边表则为入度

其他链式存储方式

十字链表（有向图）、邻接多重表（无向图）…

---

图的遍历

• 图的遍历目标是解决图的连通性问题、拓扑排序问题、关键路径问题等
• 图的遍历分为深度优先遍历DFS和广度优先遍历BFS

深度优先遍历步骤

1. 图中所有顶点状态未为访问
2. 从某个未访问的顶点出发开始访问
3. 依次从该顶点的邻接点出发深度优先遍历，无法继续下去时退回上一个顶点深度优先遍历另一个分支
4. 如果图中还有未访问顶点，重新选择一个顶点重复23过程

深度优先遍历无法遍历所有顶点时，可判定该图非连通

广度优先遍历

优先遍历一个顶点的所有分支，类似树的层次遍历，可以借助队列实现

---

最小生成树

构建连通网最小代价生成树（即带权）
构造最小生成树的算法：Prin算法和Kruskal算法

• Prin算法：从某个顶点开始，选择权值最小的边进行连接，将连起来的顶点作为一个整体，再去寻找其权值最小的边进行连接，但不能形成回路

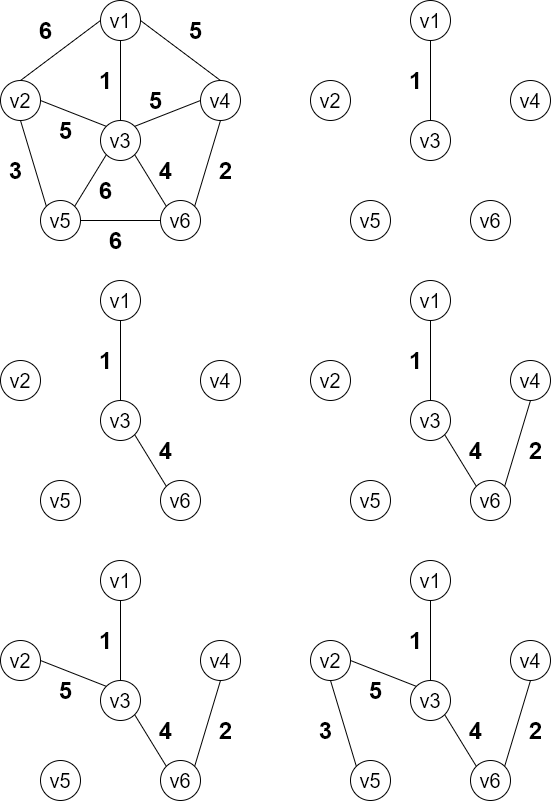
• Kruskal算法：将边按权进行排序，每次只挑选权值最小的进行连接，并且避免回路

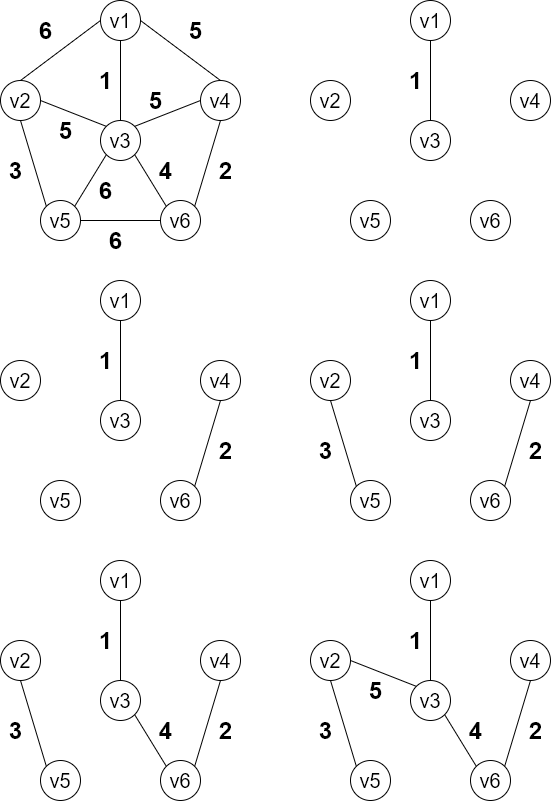
• 区别：Prin算法基于连通的选择，Kruskal算法离散的选择

---

拓扑排序

• 由某个集合上的偏序得到该集合上的全序
• AOV网：顶点表示活动，弧表示活动之间的优先关系的有向图

拓扑排序方法

1. 在有向图中找到一个没有前驱的结点输出
2. 删掉该结点
3. 重复12

---

Dijkstra算法

可用于求最短路径

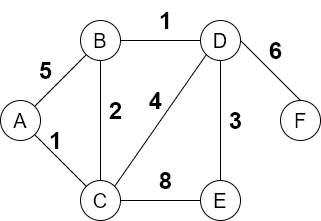
在BFS中，借助队列来进行遍历，在Dijkstra算法中，可以借助优先级队列priority queue，priority queue可以通过堆heap来实现

从A开始，加入优先级队列

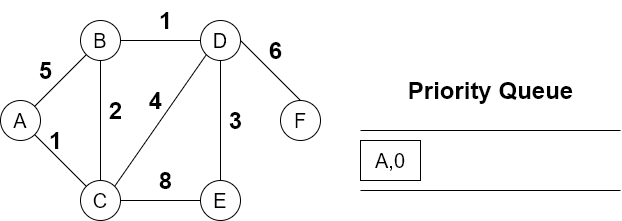
A出队，将A邻接点BC加入队列，优先级队列会自动将数据排序

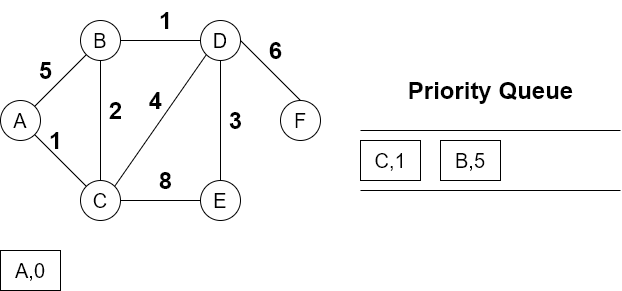
C出队作为路径，C的邻接点为BD，B已经在队列中，但还没有访问到，仍然加入队列，而A已经访问过，忽略
注意邻接点的权为路径上的权之和，比如此时B的权为AC的$1$与CB的$2$之和$3$

B出队作为路径，B的邻接点CD，C已经在路径上，忽略

D出队作为路径，D的邻接点CEF，C已经在路径上，忽略

再出队是B和D，他们已经在路径中了，丢弃，所以下一个路径是E

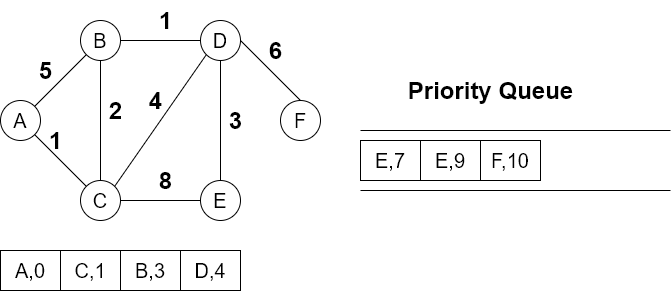
E的邻接点，没有可插入队列的了

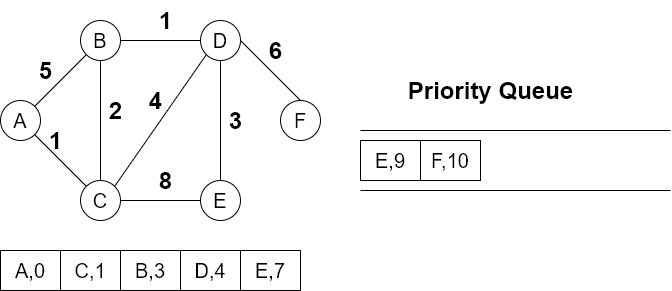
队列中的E被丢弃，下一个路径是F，队列中没有元素了，算法结束
将该路径中每个顶点的前驱记录成一个表

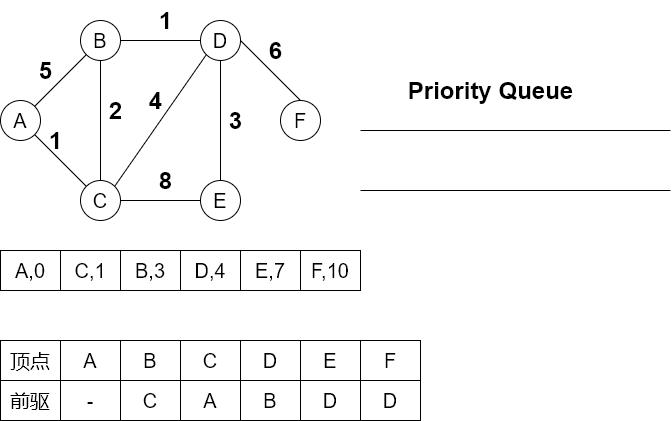
A到F的最短路径为ACBDF，长度为10

---