06/08/2020 Datastruct
一些概念
- 树:N个结点的有限集
- 结点:一个数据元素及指向子树的分支
- 结点的度:结点的子树数
- 叶子结点:度为0的结点
- 分支结点:度不为0的结点
- 树的度:树中结点的度的最大值
- 树的深度:树的最大层数
- 二叉树:每个结点至多有2个子树,且有左右之分
- 二叉树5个基本形态:空/根结点/只有左子树/只有右子树/左右子树都存在
一些性质
- 二叉树的第(i)层最多有(2^{i-1})个结点
- 深度为(k (k\geq1))的二叉树最多有(2^k-1)个结点
- 对于任何一个二叉树,如果其叶子结点数为(n_0),度为2的结点数为(n_2),则(n_0=n_2+1)
满二叉树和完全二叉树
- 满二叉树:深度为(k)且总共有(2^k-1)个结点的二叉树
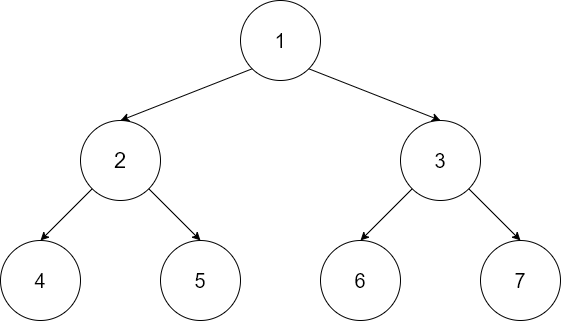
- 完全二叉树:深度为(k)且总共有(n)个结点的二叉树,当且仅当其每个结点都与深度为(k)的满二叉树从1到(n)的结点一一对应
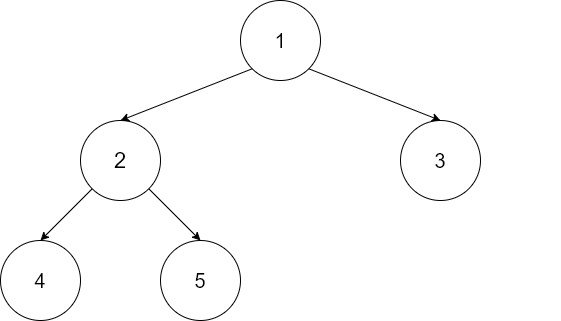
完全二叉树性质
- (n)个结点的完全二叉树的深度为(\log_{2}n+1)
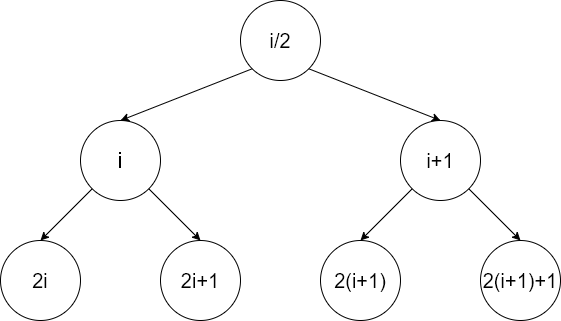
- 对于(n)个结点的完全二叉树的任一结点(i)
- 若(i=1)则为根结点,若(i>1), (i)的父结点为(i/2)
- 若(2i>n),则(i)无左子树,否则左孩子结点为(2i)
- 若(2i+1>n),则(i)无右子树,否则右孩子结点为(2i+1)
二叉树的存储结构
任何数据结构都可以用顺序存储和链式存储
二叉链表
class TreeNode<T> {
T data;
TreeNode<T> left;
TreeNode<T> right;
}
class BinTree<T>{
TreeNode<T> root;
}最常用的存储方式
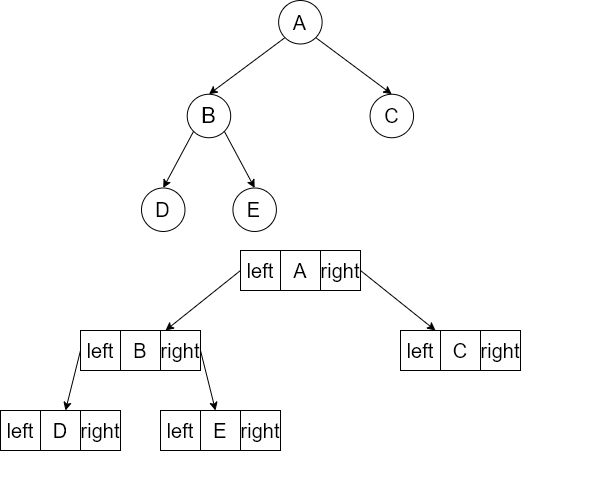
$n$个结点的二叉链表中,有$n+1$个空链域
简单顺序存储
class BinTree<T>{
T[] elements;
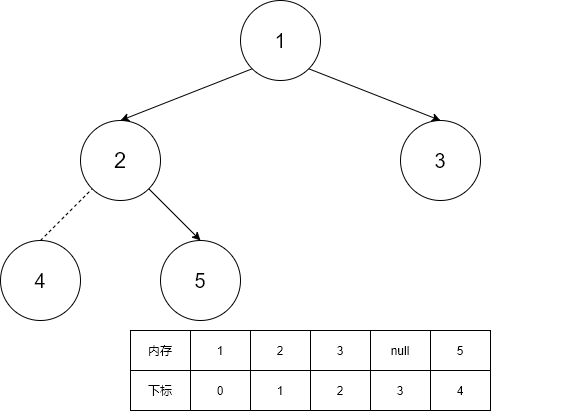
}将二叉树转为完全二叉树
虚拟出空结点
将完全二叉树上编号(i)的结点存储在数组的(i-1)位置
空结点对应的数组元素存null
如果是单边树,会很浪费空间,一般不使用这种方法
双亲表示法
class Node<T> {
T data;
int parent; //父节点的下标
}
class BinTree<T>{
Node<T>[] elements;
}每个结点都记住父结点在数组中的下标
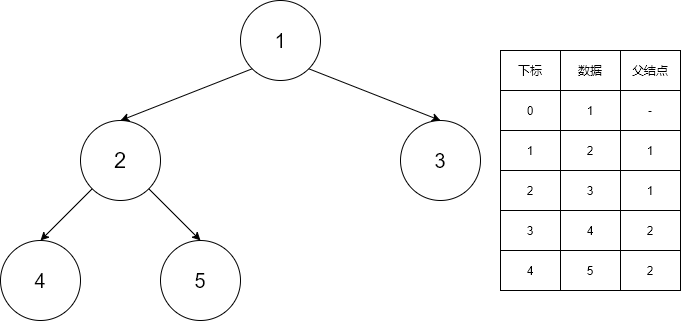
- 优点:容易找到父结点
- 缺点:找子结点需要遍历整个结构
孩子表示法
是数组和链表结合的存储方法
每个结点需要存储它的子结点在数组中的下标链表
class Node<T> {
T data;
LinkedList<T> children;
}
class BinTree<T>{
Node<T>[] elements;
}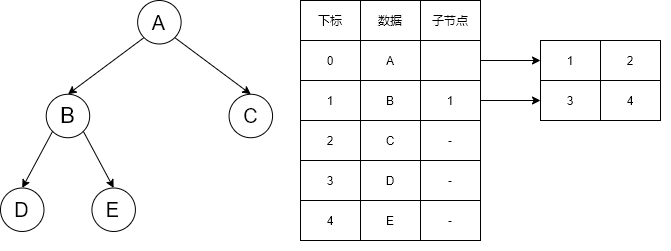
- 优点:容易找到子结点
- 缺点:找父结点不方便
带父结点的孩子链表
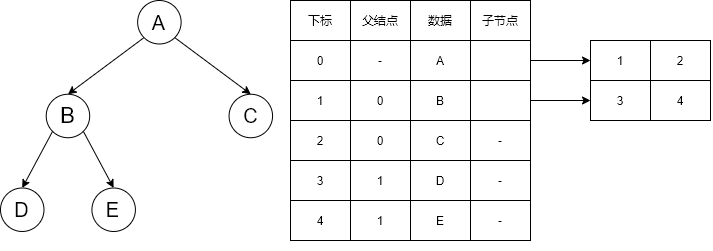
将双亲表示法和孩子表示法结合起来
class Node<T> {
T data;
LinkedList<T> children;
int parent; //父节点的下标
}
class BinTree<T>{
Node<T>[] elements;
}
兄弟孩子表示法
另一种链式存储方法
结点的左孩子为从左往右的第一个子结点,右孩子为其兄弟结点
class Node<T> {
T data;
Node<T> firstChild;
Node<T> brothers;
}
class BinTree<T>{
Node<T> root;
}常用于树转换为二叉树,森林转换为二叉树
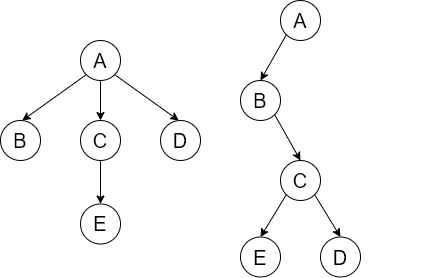
任何一个与树对应的二叉树,右子树都为空
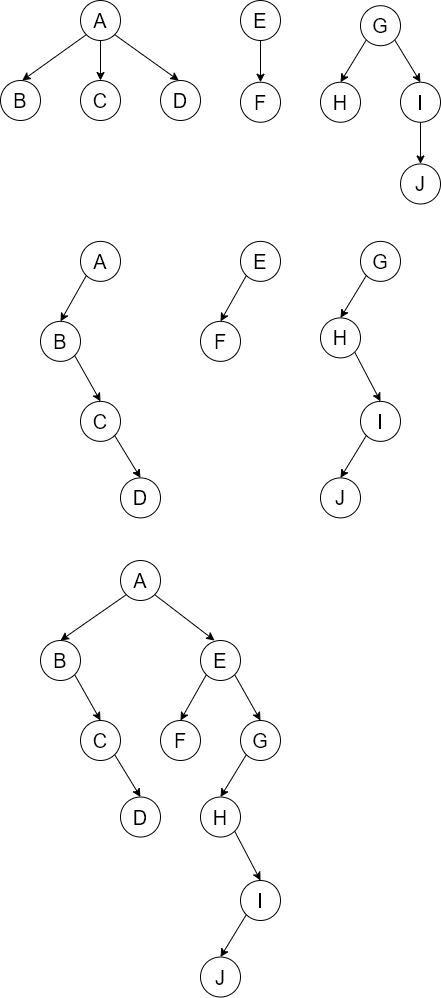
先将每个树转为二叉树,再将每个二叉树根节点连接
二叉树的遍历
以二叉链表结构为例
class TreeNode<T> {
T data;
TreeNode<T> left;
TreeNode<T> right;
}
class BinTree<T>{
TreeNode<T> root;
}先序遍历
- 递归方法
void preOrderTraversal(TreeNode<T> node) {
if (node == null) {
return;
}
System.out.println(node.data);
preOrderTraversal(node.left);
preOrderTraversal(node.right);
}- 非递归方法,使用栈
void preOrderTraversal() {
Stack<TreeNode<T>> stack = new Stack<>();
stack.push(root);
while (!stack.isEmpty()) {
TreeNode<T> node = stack.pop();
System.out.println(node.data);
// 先push右孩子再push左孩子
// 左孩子先出栈
if(node.right != null) {
stack.push(node.right);
}
if(node.left != null) {
stack.push(node.left);
}
}
}中序遍历
- 递归方法
void inOrderTraversal(TreeNode<T> node) {
if (node == null) {
return;
}
inOrderTraversal(node.left);
System.out.println(node.data);
inOrderTraversal(node.right);
}- 非递归方法使用栈
void inOrderTraversal() {
Stack<TreeNode<T>> stack = new Stack<>();
TreeNode<T> node = root;
while(node != null || !stack.isEmpty()){
while (node != null) {
stack.push(node);
node = node.left;
}
node = stack.pop();
System.out.println(node.data);
node = node.right;
}
}后序遍历
- 递归方法
void postOrderTraversal(TreeNode<T> node) {
if (node == null) {
return;
}
postOrderTraversal(node.left);
postOrderTraversal(node.right);
System.out.println(node.data);
}- 非递归方法使用两个栈
void postOrderTraversal() {
Stack<TreeNode<T>> stack1 = new Stack<>();
Stack<TreeNode<T>> stack2 = new Stack<>();
stack1.push(root);
while (!stack1.isEmpty()) {
TreeNode<T> node = stack1.pop();
stack2.push(node);
if(node.left != null) {
stack1.push(node.left);
}
if(node.right != null) {
stack1.push(node.right);
}
}
while (!stack2.isEmpty()) {
TreeNode<T> node = stack2.pop();
traversal.apply(node.data);
}
}层序遍历
- 递归方法
void levelOrderTraversal() {
int level = 1;
while (levelOrderTraversal(root, level)) {
level++;
}
}
boolean levelOrderTraversal(TreeNode<T> node, int level) {
if (node == null) {
return false;
}
if (level == 1) {
System.out.println(node.data);
return true;
}
boolean left = levelOrderTraversal(node.left, level - 1);
boolean right = levelOrderTraversal(node.right, level - 1);
return left || right;
}- 非递归方法使用队列
void levelOrderTraversal() {
Queue<TreeNode<T>> queue = new LinkedList<>();
queue.add(root);
while (!queue.isEmpty()) {
TreeNode<T> node = queue.poll();
System.out.println(node.data);
if (node.left != null) {
queue.add(node.left);
}
if (node.right != null) {
queue.add(node.right);
}
}
}深度优先遍历dfs即为先序遍历,广度优先遍历bfs即为层序遍历
如果增加一些辅助数据域,比如父结点或访问位,也可以不借助其他数据结构进行遍历
给定一个数组,按层序构建一个完全二叉树
- 递归方法
使用完全二叉树的性质,编号为$i$的结点,左孩子结点的编号为$2i$,右孩子结点的编号为$2i+1$
数组下标从0开始,树的序号从1开始,所以再加1
<T> TreeNode<T> fromLevelOrder(T[] arrays, int index) {
if (index < arrays.length) {
TreeNode<T> node = new TreeNode<>(arrays[index]);
node.left = fromLevelOrder(arrays, index * 2 + 1);
node.right = fromLevelOrder(arrays, index * 2 + 2);
return node;
}
return null;
}- 非递归方法,使用队列
<T> BinTree<T> fromLevelOrderByQueue(T[] arrays) {
BinTree<T> tree = new BinTree<>();
for (T t : arrays) {
tree.insert(t);
}
return tree;
}
void insert(T data) {
if (root == null) {
root = new TreeNode<>(data);
return;
}
Queue<TreeNode<T>> queue = new LinkedList<>();
queue.add(root);
while (!queue.isEmpty()) {
TreeNode<T> tmp = queue.poll();
if (tmp.left == null) {
tmp.left = new TreeNode<>(data);
break;
} else {
queue.add(tmp.left);
if (tmp.right == null) {
tmp.right = new TreeNode<>(data);
break;
} else {
queue.add(tmp.right);
}
}
}
}Huffman树(最优二叉树)
一些概念
- 路径:从一个结点到另一个结点之间的分支
- 路径长度:路径上的分支数
- 树的路径:从根结点到每一个结点的路径长度之和
- 带权路径长度:路径上分支数量与权值的乘积
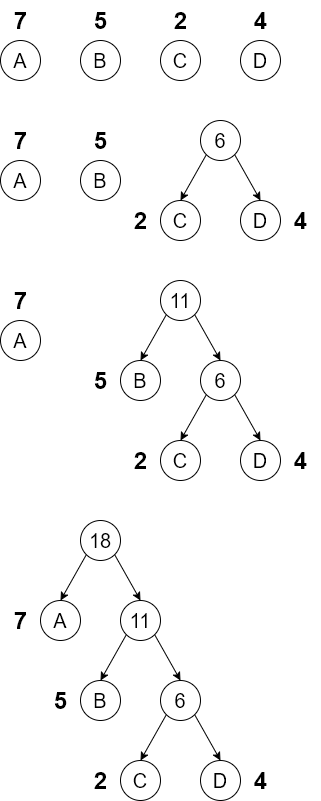
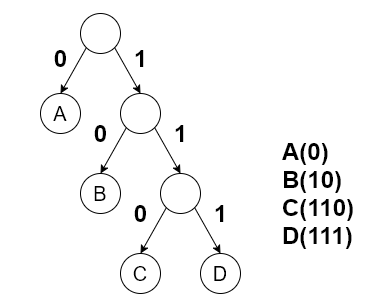
Huffman树的带权路径长度最短
Huffman树没有度为1的结点,是严格的二叉树
一些练习
度为2的树与二叉树的区别
- 二叉树的度最大值为2,二叉树的子节点有左右顺序,而度为2的树子节点不一定有序
$n$个结点的二叉链表中有多少空链域
- $n$个结点的二叉链表中有$2n$个链域,除了根结点每个结点都占用一个链域,即$n-1$个链域,则空链域为$2n-(n-1)=n+1$个
一个含有$n$个结点的$k$叉树,可能的最大深度和最小深度是多少
- 最大为深度为$n$(单边树),最小深度为$log_{k}n+1$(完全$k$叉树)
对于非叶子结点都有左右子树的二叉树,有$n$个叶子结点的树中总共多少个结点
- 对于任何二叉树,度为$0$的结点$n_0$和度为$2$的结点$n_2$有$n_0=n_2+1$,所以该树共有$n+n-1=2n-1$个结点
找出满足下列条件的二叉树
- 先序和中序遍历,得到的结果相同
- 后序和中序遍历,得到的结果相同
- 先序和后续遍历,得到的结果相同
- 1无左子树,2无右子树,3仅一个结点